Funktoren
Wie man sich nach dem letzten Eintrag bereits vorstellen kann, sind Kategorien für sich genommen noch nicht besonders hilfreich. Was fehlt ist eine Möglichkeit, unterschiedliche Kategorien miteinander zu verbinden. Konkret bedarf es einem Mittel um Beziehungen zwischen Kategorien herzustellen.
An dieser Stelle betreten die Funktoren die Bühne:
"Every sufficiently good analogy is yearning to become a functor."
- John Baez
Ein Funktor ist nämlich eine Abbildung zwischen Kategorien mit der besonderen Eigenschaft, dass alle Eigenschaften der Domänen-Kategorie in die Co-Domänen-Kategorie übertragen werden.
Zur besseren Vorstellung kann man auch sagen ein Funktor ist ein Container für Daten mit definierten Eigenschaften.
In der Konkreten Notation sieht das dann folgendermaßen aus:
Die Daten
Sei \(F:\mathcal{C}\rightarrow\mathcal{D}\) so gilt
$$A\in\lVert\mathcal{C}\rVert\Rightarrow F(A)\in\lVert\mathcal{D}\rVert$$
"ist \(A\) ein Objekt in \(\mathcal{C}\), so ist \(F(A)\) ein Objekt in \(\mathcal{D}\)"
für alle Objekte in \(\mathcal{C}\) und
$$f\in Morph(\mathcal{C})\Rightarrow F(f)\in Morph(\mathcal{D})$$
"ist \(f\) Morphismus in \(\mathcal{C}\), so ist \(F(f)\) Morphismus in \(\mathcal{D}\)"
für alle Morphismen in \(\mathcal{C}\).
Die Eigenschaften
Es gelten folgende Eigenschaften für Daten der Form \(F(A)\)
$$F(Id_A)=Id_{F(A)}$$
für alle Identitätsmorphismen von \(\mathcal{C}\).
Im Grunde soll diese Eigenschaft nur sicherstellen, dass alle Identitätsmorphismen aus der Domänen-Kategorie gleichermaßen in der Co-Domänen-Kategorie existieren.
Sind zudem \(f:A\rightarrow B\) und \(g:B\rightarrow C\) Morphismen von \(\mathcal{C}\) und \(\circ_{\mathcal{C}}\) die Komposition in \(mathcal{C}\) sowie \(\circ_{\mathcal{D}}\) die Komposition in \(\mathcal{D}\) dann gilt folglich
$$F(g\circ_{\mathcal{C}}f)=F(g)\circ_{\mathcal{D}}F(f)$$
Werden also zwei Morphismen in der Domänen-Kategorie von \(F\) komponiert hat dies die gleiche Bedeutung, wie wenn man die durch \(F\) abgebildeten Morphismen in der Co-Domänen-Kategorie komponiert.
Die beiden Eigenschaften werden in der Regel auch als Funktoren-Gesetze ("functor-laws") bezeichnet.
Kommutative Diagramme
In der Kategorientheorie werden Morphismen und ihre Kompositionen gerne in Form von kommutativen Diagrammen dargestellt. Diese bestehen aus Objekten sowie Pfeilen und geben einen einfachen Überblick über beispielsweise Äquivalenzen von Kompositionen.
Das Kommutationsdiagramm von Funktoren sieht folgendermaßen aus:
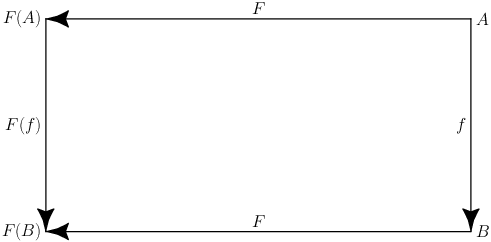
Es lässt sich leicht herauslesen dass
$$F\circ f\Leftrightarrow F(f)\circ F$$
gelten muss. Hierzu brauchen wir bloß dem Pfeil am rechten Rand folgen und anschließend dem unteren Pfeil für die linke Hälfte der Gleichung, bzw. dem oberen und anschließend dem linken Pfeil für die rechte Hälfte der Gleichung.

In kommutativen Diagrammen gilt folgende Regel:
Gibt es von einem Objekt mehrere Weg zu einem anderen, muss die Komposition der betreffenden Morphismen identisch sein.
Funktoren in der Praxis
Wie gestaltet sich nun ein solcher Funktor in der praxis aus und mit welchen Funktoren haben wir möglicherweise bereits zu tun, ohne es zu wissen?
In der Praxis bedeutet das, dass etwas um ein Funktor zu sein eine Fuktion implementieren muss, welche die Abbildung von Domäne zu Co-Domäne durchführt. Diese Funktion wird in der Regel mit fmap oder map bezeichnet. Einzige Anforderung an diese Funktion ist, dass die Funktoren-Gesetze (s. oben) von ihr eingehalten werden.
Diese Funktion hat üblicherweise folgende Signatur:
fmap :: Functor f => (a -> b) -> f a -> f b
Sprich die Funktion nimmt zwei parameter; einen Morhpismus von a nach b sowie einen Funktor von a und gibt einen Funktor von b zurück.
Die Funktion penetriert also den Funktor um auf die enthaltenen Daten zuzugreifen und stellt sicher, dass das Ergebnis des Morphismus wieder als Funktor gleicher Art zurück kommt.
Wer bei Erwähnung des Funktionsnamens hellhörig geworden ist, der kann sich an dieser Stelle bestätigt fühlen: Listen sind Funktoren (zumindest in den meisten Programmiersprachen). Allerdings sind Listen nicht die einzigen Funktoren die sich in Kotlin standard-Typen verstecken, auch Any? und alle anderen nullable-Typen sind Funktoren, hier heißt die Funktion allerdings ?. anstatt map.
Zur Überprüfung hier der genannten Beispiele wollen wir die Listen einzeln betrachten.
- listOf(x) entpricht \(F(x)\) und bildet das Objekt \(x\) aus der Kategorie \(\mathcal{X}\) auf das Objekt \([x]\) aus der Kategorie \(\mathcal{L}\) ab.
- Sei listOf(1,2,3) gegeben, und sei fun f(x: Int) = x+1 so gilt listOf(1,2,3).map(::f)==listOf(2,3,4), map entspricht also \(F(f)\) und bildet einen Mophismus \(f\) aus der Kategorie \(\mathcal{X}\) auf den entsprechenden Morphismus in \(\mathcal{L}\) ab.
- Sei fun <A> A.id() = this, es gilt listOf(1,2).id()==listOf(1.id(),2.id()).
- Sei fun <A,B,C> compose(f: (A)->B, g: (B)->C): (A)->C = {input -> g(f(input))},sei zudem fun f(x: Int) = x+1 und fun g(x: Int) = x*3. Es gilt listOf(1,2).map(compose(f,g))==listOf(compose(f,g)(1),compose(f,g)(2))
Damit sind alle oben genannten Vorraussetzungen erfüllt und die Listen damit nachweislich Funktoren.







