Multi- und Polymorphismen
Multipmorphismus und Binäres Produkt
Zwei Objekten einer Kategorie kann ein Produkt zugeordnet werden, so stellt beispielsweise ein Satz Pokerkarten das kartesische Produkt aus Rängen
$$R={2,3,4,5,6,7,8,9,10,J,K,Q,A}$$
und Farben
$$F=\{\heartsuit,\diamondsuit,\spadesuit,\clubsuit\}$$
dar. Jede Kombination aus diesen beiden Mengen ergibt genau eine Karte. Die Menge der Pokerkarten wird \(R\times F\) geschrieben. Ein alternatives Beispiel findet sich in der Welt der Datenbanken in der SELECT * FROM A,B das kartesische Produkt aus den Tabellen A und B bildet. Die wichtigste Eigenschaft solcher Produkte ist die, dass es zwei Morphismen \(p_1:A\times B\rightarrow A\) und \(p_2:A\times B\rightarrow B\) gibt. Diese beiden Morphismen ordnen dem Produkt seine Komponenten zu, im Falle der Pokerkarten wären dies die Morphismen \(r:R\times F\rightarrow R\) bzw. \(f:R\times F\rightarrow F\) die einer Karte ihre Farbe bzw. ihren Rang zuordnen.
Auf Basis dieser Projektionen können wir nun den Multimorphismus definieren:
Definition
Es sind \(A\) und \(B\) Objekte in der Kategorie \(\mathcal{C}\). Das Produkt \(A\times B\) ist gegeben durch zwei Morphismen Es sind und Objekte in der Kategorie . Das Produkt ist gegeben durch zwei Morphismen \(p_1:A\times B\rightarrow A\) und \(p_2:A\times B\rightarrow B\) die folgende Eigenschaft erfüllen. Für jedes Objekt \(Z\) mit Morphismen \(f: Z\rightarrow A\) und \(g:Z\rightarrow B\) gibt es einen Morphismus \(\langle f,g\rangle :Z\rightarrow A\times B\) mit \(f=p_1\circ\langle f,g\rangle\) und \(g=p_2\circ\langle f,g\rangle\). Der Morphismus \(\langle f,g\rangle\) heisst dann Multimorphismus.
Zum besseren Verständnis dieses Textes dient das kommutative Diagramm:
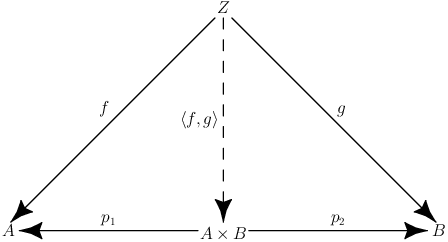
Mit Bezug auf unser Beispiel der Pokerkarten bedeutet das, sobald von einem Objekt \(Z\) Morphismen existieren, welche von diesem Objekt auf die Menge \(R\) der Ränge bzw. die Menge \(F\) der Farben abbilden. So folgt daraus, dass die Kombination dieser beiden Morphismen einen Multimorphismus hervorbringt welcher von \(Z\) direkt auf eine Pokerkarte abbildet. So könnte \(Z={x\in\mathbb{N}:1\leq x\leq 52}\) gelten und \(f\) und \(g\) wie folgt definiert sein:
$$f: x\mapsto \begin{cases}2 & x\equiv_{13}1\\3 & x\equiv_{13}2\\\vdots\\A & x\equiv_{13}0\end{cases}$$
$$g:x\mapsto \begin{cases}
\heartsuit & 1\leq x\leq 13\\
\diamondsuit & 14\leq x\leq 26\\
\spadesuit & 27\leq x\leq 39\\
\clubsuit & 40\leq x\leq 52\end{cases}$$
Der dadurch definierte Multimorphismus \(\langle f,g\rangle\) ist trivialerweise \(\langle f,g\rangle: x\mapsto (f(x),g(x))\), also der Morphismus der eine Zahl aus \(Z\) auf das Paar aus Rang und Farbe – welches wiederum eine Karte definiert – abbildet. Die Vorraussetzung, dass die beiden Projektionsmorphismen \(p_1\) und \(p_2\) die entstandene Karte wieder auf genau den gleichen Rang / die gleiche Farbe abbilden wie \(f\) bzw. \(g\) ist offensichtlich gegeben.
Polymorphismus und Binäres Ko-Produkt
In der Kategorientheorie lässt sich zu jedem kommutativen Diagramm ein dazu duales Diagramm bilden, indem man alle Pfeile umdreht. Aus dem binären Produkt ensteht auf diese Weise das binäre Ko-Produkt.
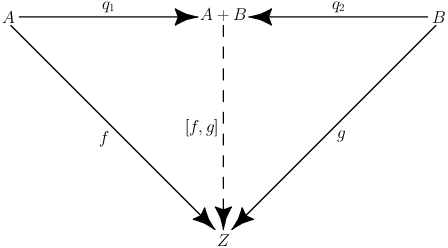
Definition
Es sind \(A\) und \(B\) Objekte in der Kategorie \(\mathcal{C}\). Das Ko-Produkt \(A+B\) ist gegeben durch zwei Morphismen \(q_1: A\rightarrow A+B\) und \(q_2: B\rightarrow A+B\) die folgende Eigenschaft erfüllen. Für jedes Objekt \(Z\) mit Morphismen \(f:A\rightarrow Z\) und \(g:B\rightarrow Z\) gibt es einen Morphismus \([f,g]:A+B\rightarrow Z\) mit \(f=[f,g]\circ q_1\) und \(g=[f,g]\circ q_2\). Der Morphismus \([f,g]\) heisst dann Polymorphismus bzw. Ko-Multimorphismus.
Auch wenn es zunächst sehr ähnlich aussieht, ist das Ko-Produkt etwas vollkommen anderes als das Produkt. Ausgehend von zwei Mengen entspräche es der disjunkten Vereinigung der beiden Mengen. Sind die beiden Mengen disjunkt – haben also keine gemeinsamen Elemente – ist das äquivalent zur normalen Vereinigung der Mengen \(A\cup B\). Haben die beiden Mengen jedoch gemeinsame Elemente müssen diese in irgendeiner Form "markiert" werden um deren Ursprung feststellen zu können (\(x_Aeq x_B\)).
Das Ko-Produkt aus \(R\) und \(F\) ist zum Beispiel
$$R+F=\{2,3,4,5,6,7,8,9,10,J,Q,K,A,\heartsuit,\diamondsuit,\spadesuit,\clubsuit\}$$
Ein ganz besonderes Objekt dagegen ist der Polymorphismus \([f,g]: A+B\mapsto Z\). Als duales Objekt zum Multimorphismus ist seine Domäne die disjunkte Vereinigung der Domänen von \(f\) und \(g\). Durch diesen Umstand kann der Polymorphismus Elemente aus beiden Domänen auf seine Ko-Domäne abbilden. Definiert ist er dabei äquivalent zu einem if/else-Statement:
$$[f,g]: x\mapsto \begin{cases}
f(x) & x\in A\\
g(x) & x\in B
\end{cases}$$
sprich \([f,g](x)\) ist identisch mit \(f(x)\) wenn \(x\) aus \(A\) stammt und identisch mit \(g(x)\) wenn \(x\) aus \(B\) stammt.
Preview
Im nächsten Eintrag gehts um Produkt- und Ko-Produktmorphismen.







