F-Algebren
Definition
Sei \(F: \mathcal{C}\rightarrow \mathcal{C}\) ein Endofunktor. Eine F-Algebra ist ein Paar \((A,\alpha)\), wobei \(A\) ein Objekt von \(\mathcal{C}\) und \(\alpha : F(A)\rightarrow A\) ein Morphismus von \(\mathcal{C}\) ist.
F-Algebra ist also nur eine Funktion von einem Endofunktor zu einem Objekt, oder vielmehr das Paar aus einem Objekt und einer Funktion von ihm -- zum Funktor gehoben -- zu sich selbst.
Versuchen wir, dieses Konzept anzuwenden, indem wir eine Multiplikationsalgebra konstruieren. Dafür definieren wir unseren Endofunktor als \(F: A\mapsto A\times A\). Der Funktor bildet also eine gegebene Menge auf ihre Quadratmenge ab, d.h. \(\mathbb{N}\) würde auf \(\mathbb{N}\times\mathbb{N}\) abgebildet werden. Auf einer Quadratmenge wie dieser wird die Multiplikation \(\alpha: \mathbb{N}\times\mathbb{N}\rightarrow\mathbb{N}\) wie folgt definiert \(\alpha:x,y\mapsto x*y\). Die resultierende Algebra würde dann als \((\mathbb{N}, *)\) notiert.
Operationen auf F-Algebren
F-Algebren können aufeinander abgebildet werden, dies geschieht für einen bestimmten Funktor \(F\) innerhalb der Kategorie \(Alg(F)\). Innerhalb dieser Kategorie sind die Objekte die F-Algebren \((A,\alpha)\) und die Homomorphismen \(h: (A,\alpha)\rightarrow(B,\beta)\) die Morphismen.
Wenn wir uns mit Katamorphismen beschäftigen, werden wir sehen, dass wir einen F-Algebra-Homomomorphismus unter \(F: A \rightarrow 1 + \mathbb{N}\times A\) von der F-Algebra der Listen \((\mathbb{L}, [I_{[]}, +])\) (wobei \(+\) die Funktion ist, die zwei Listen verkettet) zur F-Algebra der Zahlen und ihrer Produkte \((\mathbb{N}, [I_1, *])\). Dieser Homomorphismus stellt die multiplikative Kombination (oder das Produkt) der Listenelemente dar.
F-Ko-Algebren
Sei \(F: \mathcal{C}\rightarrow \mathcal{C}\) ein Endofunktor.Eine F-Co-Algebra ist ein Paar \((A,\alpha)\), wobei \(A\) ein Objekt von \(\mathcal{C}\) und \(\alpha : A\rightarrow F(A)\) ein Morphismus von \(\mathcal{C}\) ist.
Das bedeutet, dass, wenn \((A,\alpha)\) eine F-Algebra ist, \((A,\alpha^{-1})\) eine F-Co-Algebra ist, wenn die inverse Funktion \(\alpha^{-1}\) existiert.
Initiale F-Algebra
Eine F-Algebra \((A,\alpha)\) wird initial genannt, wenn für jede F-Algebra \((B,\beta)\) in der Kategorie \(Alg(F)\) genau ein Morphismus \(h: (A,\alpha)\rightarrow(B,\beta)\) existiert.
Die F-Algebra der Listen ist ein Beispiel für eine initiale F-Algebra, das sagt uns, dass wir mit einer Liste von Objekten im Grunde alles machen können, wobei "alles machen" bedeutet, dass es einen Morphismus für all diese Operationen gibt.
Finale F-Algebra
Eine F-Algebra \((B,\beta)\) wird als final bezeichnet, wenn für jede F-Algebra \((A,\alpha)\) in der Kategorie \(Alg(F)\) genau ein Morphismus \(h: (A,\alpha)\rightarrow(B,\beta)\) existiert.
F-Algebra-Homomorphismus
Sei \(\mathcal{C}\) eine Kategorie und \(F:\mathcal{C}\rightarrow\mathcal{C}\\) ein Endofunktor. Ein Morphismus ist genau dann ein F-Algebra-Homorphismus, wenn das folgende Diagramm kommutiert
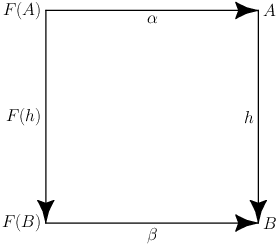
Die folgende Gleichung lässt sich aus dem Diagramm ablesen:
$$h\circ \alpha = \beta\circ F(h)$$
Preview
Im nächsten Artikel kommen wir endlich zur Sache und betrachten den rekursiven Zerfall mit Hilfe von Katamorphismen.







