Productmorphism
Definition
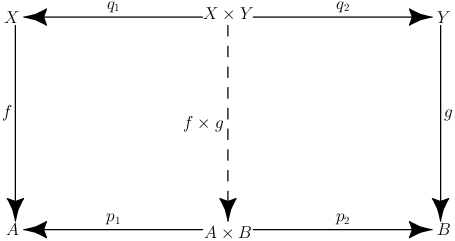
Let \(f:X\rightarrow A\) and \(g:Y\rightarrow B\) then the productmorphism \(f\times g: X\times Y\rightarrow A\times B\) is defined with \(q_1:X\times Y\rightarrow X\), \(q_2: X\times Y\rightarrow Y\), \(p_1:A\times B\rightarrow A\) and \(p_2:A\times B\rightarrow B\) as well as the relationships \(f\circ q_1= p_1\circ (f\times g)\) and \(g\circ q_2= p_2\circ (f\times g)\) as follows: \(f\times g= \langle f\circ q_1, g\circ q_2\rangle\).
This relationship becomes clear when looking at the commutative diagram for multimorphisms
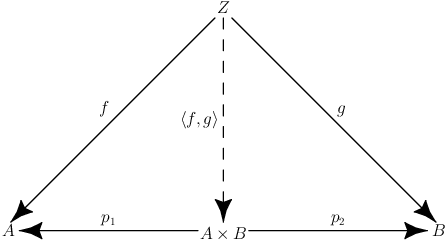
If we replace \(Z\) by \(X\times Y\) and integrate \(q_1:X\times Y\rightarrow X\) and \(q_2:X\times Y\rightarrow Y\) as intermediate steps over \(X\) and \(Y\) respectively, we obtain the following diagram:
Co-Productmorphism
As with multimorphism, the dual concept of co-productmorphism also exists for the productmorphism
We obtain the co-productmorphism analogous to the above by replacing \(Z\) with \(X+Y\) in the commutative diagram of the polymorphism and then introducing \(p_1=X\rightarrow X+Y\) and \(p_2=Y\rightarrow X+Y\) as intermediate steps via \(X\) and \(Y\), respectively.
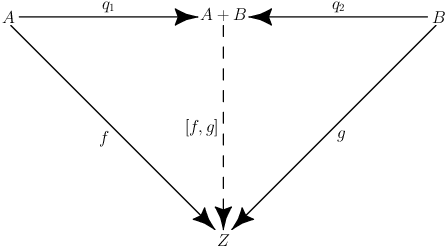
As a result we get the following diagram
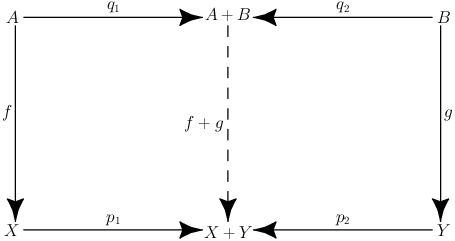
Definition
Let \(f:X\rightarrow A\) and \(g:Y\rightarrow B\) then the co-productmorphism \(f+g:A+B\rightarrow X+Y\) is defined with \(q_1:A\rightarrow A+B\), \(q_2: B\rightarrow A+B\), \(p_1:X\rightarrow X+Y\) and \(p_2:Y\rightarrow X+Y\) as well as the relationships \(p_1\circ f= (f+g)\circ q_1\) and \(p_2\circ g=(f+g)\circ q_2\) as follows: \(f+g=[p_1\circ f, p_2\circ g]\).
The only difference to the polymorphism is that the co-productmorphism maps to the same co-domain in both cases.
Preview
Next time you will get everything about F-algebras, so we will have all the basics together to define recursive morphisms... exciting!







