F-Algebras
Definition
Let \(F: \mathcal{C}\rightarrow \mathcal{C}\) be a endofunctor. An F-Algebra is a pair \((A,\alpha)\) where \(A\) is an object of \(\mathcal{C}\) and \(\alpha : F(A)\rightarrow A\) is a morphism of \(\mathcal{C}\).
So F-algebra is just a function from an endofunctor to an object, or rather the pair of a object and a function from it -- lifted to the functor -- to itself.
Let's try and apply this concept, we're going to construct a multiplication algebra. For this we define our endofunctor as \(F: A\mapsto A\times A\). So the functor maps a given set to it's squared set i.e. \(\mathbb{N}\) would be mapped to \(\mathbb{N}\times\mathbb{N}\). On a squared set like this the multiplication is defined \(\alpha: \mathbb{N}\times\mathbb{N}\rightarrow\mathbb{N}\) as follows \(\alpha:x,y\mapsto x*y\). The resulting algebra would then be noted as \((\mathbb{N}, *)\).
Operating on F-algebras
F-algebras can be mapped onto one another, this happens for a given functor \(F\) inside the category \(Alg(F)\). Inside this category the objects are the F-algebras \((A,\alpha)\) and the homomorphisms \(h: (A,\alpha)\rightarrow(B,\beta)\) the morphisms.
We will see when dealing with catamorphisms, that we can construct a F-algebra-homomorphism under \(F: A \rightarrow 1 + \mathbb{N}\times A\) from the F-algebra of lists \((\mathbb{L}, [I_{[]}, +])\) (with \(+\) being the function that concatenates two lists) to the F-algebra of Numbers and their products \((\mathbb{N},[I_1, *])\). This homomorphism represents the multiplicative combination (or product) of the list-elements.
F-co-algebras
Let \(F: \mathcal{C}\rightarrow \mathcal{C}\) be a endofunctor. An F-co-algebra is a pair \((A,\alpha)\) where \(A\) is an object of \(\mathcal{C}\) and \(\alpha : A\rightarrow F(A)\) is a morphism of \(\mathcal{C}\).
That means that, if \((A,\alpha)\) is an F-algebra, \((A,\alpha^{-1})\) is an F-co-algebra if the functions inverse \(\alpha^{-1}\) exists.
Initial F-algebra
An F-algebra \((A,\alpha)\) is called initial if for every F-algebra \((B,\beta)\) in the category \(Alg(F)\) there exists exactly one morphism \(h: (A,\alpha)\rightarrow(B,\beta)\).
The F-algebra of lists is an example of an initial F-algebra, this tells us that we can do basically anything with a list of objects, where 'do anything' means that there is a morphism for all these operations.
Final F-algebra
An F-algebra \((B,\beta)\) is called final if for every F-algebra \((A,\alpha)\) in the category \(Alg(F)\) there exists exactly one morphism \(h: (A,\alpha)\rightarrow(B,\beta)\).
F-algebra-homomorphism
Let \(\mathcal{C}\) be a category and \(F:\mathcal{C}\rightarrow\mathcal{C}\) an endofunctor. A morphism is exactly then a F-algebra-homomorphism if the following diagram commutates
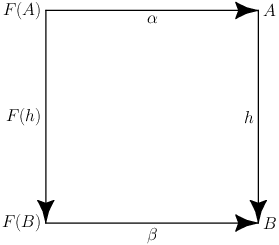
The following equation can be read from the diagram:
$$h\circ \alpha = \beta\circ F(h)$$
Preview
In the next article we'll finally get down to real business and look at recursive collapse using catamorphisms.







